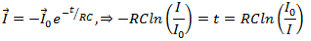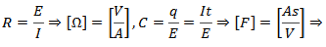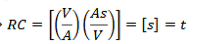A defibrillator is used to depolarize the pacemaker cells, allowing the sinoatrial node to reestablish a normal rhythm. A heart enters ventricular fibrillations and requires 30 amps. In essence, the defibrillator is a discharging capacitor, of C farads, across a patient with a resistance of R ohms. If the defibrillator started at a full charge, emitting 30 amps, how much time elapses before the current drops below 25 amps?

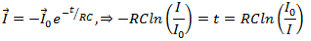
Eq. 1 – Discharge Formula

Loading ...
Correct Answer: A. R * C * ln(6/5) * s
You can answer this question quickly by dimensional analysis. The natural log is dimensionless yielding us 2 set of 2 choices. We are looking for time, units of seconds. One electrical value that contains seconds is current.
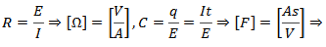
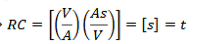
This leaves answers A and B. You should know with a discharging capacitor at time RC = Tc the value of the discharged capacitor is 37% (e-1) its initial value. 0.37 != (25/30) leaving answer choice A.
For those who would like to remember the discharge formula its:
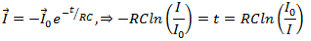
All you would need to do is plug in the values and rearrange until you arrive at answer choice A.
300 volts or proportionally 0.4 A/kg is a good estimate of how much charge is needed to restart the heart. You can calculate a lower 10 ohms resistance for the heart, from the required current and voltage.
Get it right? Tweet at us:
Subscribe below to receive the MCAT Question of the Day delivered straight to your inbox every morning.
Photo attributed to ScientificRelevance.