In which situation would a person would weigh the most?

Loading ...
Correct Answer: C. On the Earth with no air pressure.
The gravitational formula tells us that her weight is essentially:
F = (GmM / r2)
where G is the gravitational constant, M is the mass of the big body, m is the mass of the little body, and R is the distance from the two centers. Near the surface of Earth, around sea level, we approximate this as F = mg. We are allowed to obtain this approximation of g, because the small body’s mass is negligible compared to the bigger body’s mass. The remaining values are constants, and we obtain a value for g of 9.8 m/s2 . We will need to decide if each of the condition increases her weight or decreases her weight.
A.) We know that the Moon has a smaller mass than Earth, so her weight will decrease. In fact her weight on the Moon is around 1/7 of that on Earth. It’s a fun number to know.
B.) We increase the value of R to something above sea level. In comparison to the radius of the Earth, it’s not that much, but it is still enough to lower her weight.
C.) If the Earth had no air pressure, our weight calculation is unchanged. Notice how the gravity equation has no value for air pressure or density. Every time we ‘calculate’ weight we are actually leaving off those forces.
D.) Finally she would like to keep her volume but change her density to that of helium’s. We know that the density of helium is lighter than the density of air, and by extension ourselves. Let’s arbitrarily say the density of He is 0.5 the density of us. Density is just the mass over the volume. Her volume is kept constant, so her new mass is a fraction of what it initially was. This in turn will lower her weight.
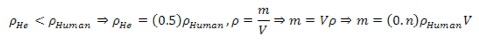
Except for case C.) her weight decreases in each situation. This makes her the heaviest when there is no pressure on the Earth, and even heavier when we consider it.
Get it right? Tweet at us:
Subscribe below to receive the MCAT Question of the Day delivered straight to your inbox every morning.