[php snippet=1]
A person, of mass 70 kg, decides to do a push up. If his arms are 7/8 up the length of his body, how much force will he need to exert to accomplish one push up?

Loading ...
Correct Answer: B. 400 N
We can set up a free body diagram representing the situation.
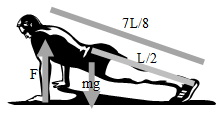
To solve this problem you could use the conservation of work and find the required work to lift himself up against gravity. The distance will be the hypotenuse times the sine, soh-cah-toa.
[latex]W=\overrightarrow{F}\cdot \overrightarrow{d},\ \ W_g=W_F\Rightarrow mg\frac{L}{2}sin\theta =F\frac{7L}{8}sin\theta \Rightarrow[/latex]
[latex]F=mg\frac{4}{7}[/latex]
You could also solve this problem with the understanding of torque. The person is virtually a ridged body, with the point of rotation placed at his feet. While he does this pushup he will be in rotational equilibrium. That means the if his butt move up, his head will also move up at the same rate. With that said the torque on his weight must equal the torque he exerts.
[latex]\overrightarrow{\tau }{\rm =}\overrightarrow{{\rm r}}{\rm \times }\overrightarrow{{\rm F}},\ \ {|\overrightarrow{\tau }}_F|=|{\overrightarrow{\tau }}_w|\Rightarrow F\frac{7L}{8}=mg\frac{L}{2}\ \Rightarrow[/latex][latex]F=mg\frac{4}{7}\Rightarrow \left(70\right)\left(10\right)\left(\frac{4}{7}\right)=400\ {\rm N}[/latex]
It is interesting to note that you only lift a little bit more than half your weight when you execute a pushup.
Get it right? Tweet at us:
Subscribe below to receive the MCAT Question of the Day delivered straight to your inbox every morning.