Falling for You

Correct Answer: C. 500 m

First we will need to calculate the force of 500 kg of weight. This is simply 5 kN. Next we will need to find the final speed required to produce 5 kN of force. We will use momentum to do so. Given 5 kN we can find a momentum of 5 kPa. Momentum is mass times velocity, allowing use to calculate a required velocity of 100 m/s.

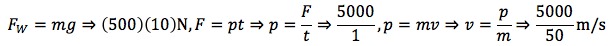
Finally we need the height of the free-fall. We know that free fall will give an equation of height equals (1/2)10t². Where 10 is the acceleration due to gravity.

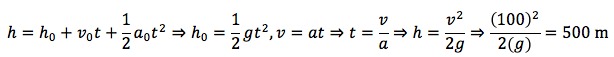
To calculate the time we can use velocity is equal to acceleration times time. This will yield a time of 10 seconds. We put our time in our height equation to yield a height of 500 meters
We could also find the answer using the conservation of energy. The kinetic energy must equal potential energy.

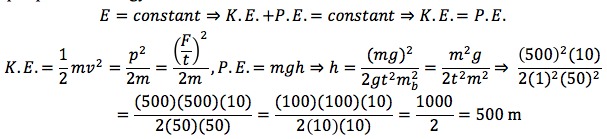
500 meters is taller than the empire state building!

Subscribe below to receive the MCAT Question of the Day delivered straight to your inbox every morning.