Excess Reagent
[php snippet=3]
Which of the following is the correct way to dispose of excess reagent?
Subscribe below to receive the MCAT Question of the Day delivered straight to your inbox every morning.
[php snippet=3]
Which of the following is the correct way to dispose of excess reagent?
[php snippet=3]
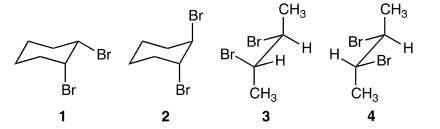
Which of the following molecules do not rotate the plane of plane-polarized light?
[php snippet=3]
Describe the reaction below.
PCl3(g) + Cl2(g) -> PCl5(g); Delta(Hf) = -87.9kJ/mol
[php snippet=3]
A high intensity peak in the mass spectrum of 2,2-dimethylpentane is observed at m/z 57. What chemical species does this peak represent?
[php snippet=3]
During the reaction to form ammonia from nitrogen and hydrogen according to the reaction: N2(g) + 3 H2(g) <-> 2 NH3(g), ammonia was being produced at the rate of 1.50 mol.L-1.s-1.
What were the respective rates of consumption of nitrogen and hydrogen at this time?
[php snippet=3]
(Fill in the blanks) Benzoic acid can be extracted into water from an organic solvent using _________ and then removed from the water into an organic solvent by the addition of _________.
[php snippet=3]
Mendel’s second law, the Law of Independent Assortment, states that each trait assigned to offspring is done so without regard to any other trait assigned. In a dihybrid cross of two dogs, one that is black with a short tail and the other that is white with a long tail, the inheritance of one fur color is not dependent upon the inheritance of tail length. Assuming that black fur is dominant and a long tail is dominant and each parent is homozygous for each trait, how many offspring in the F2 generation will be white with a short tail?
[php snippet=3]
Which statement about the following equilibrium reaction is true?

[php snippet=3]
Galvanizing is a process used to protect steel by applying a sacrificial coating? Which metal is used in galvanizing?
[php snippet=3]
Which of the following is closest to the bond angle of an sp2-hybridized carbon atom?